What Best Describes the Conservation Law Associated With Bornoullis Equation
35 static pressure dynamic pressure total pressure Every point in a steadily flowing fluid regardless of the fluid speed at that point has its own unique static pressure p and dynamic pressure q. This law is analogous to the conservation of charge in a situation where total charge is originally zero and equal amounts of positive and negative charge must be created in a reaction to keep the total zero.
Continuity equation can take the form Related Questions on Hydraulics and Fluid Mechanics In a two dimensional incompressible steady flow around an airfoil the stream lines are 2 cm apart at a great distance from the airfoil where the velocity is 30 msec.

. The acceleration of the center of mass is zero. 4 Energy can change from one type to another. My understanding is the total pressure and energy are related and remain constant for free horizontal flow of an ideal fluid.
The formula for Bernoullis principle is given as follows. Basica the equation of Bernoulli is the integral of the equation of Euler. Write out and explain the physical meaning of each term in Bernoulli.
It puts into a relation pressure and velocity in an inviscid incompressible flow. MEC 104 Quiz 3. It is one of the most importantuseful equations in fluid mechanics.
- Conservation Laws and Bernoullis Equation. We review their content and use your feedback to keep the quality high. What law do we derive Bernoullis Equation from.
Rho dvdt-grad p with rho the density v the velocity and p the pressure which is valid for a frictionless flow. Bernoullis principle is based on the law of conservation of A Angular momentum B Linear momentum C Mass D Energy Medium Open in App Solution Verified by Toppr Correct option is D. It puts into a relation pressure and velocity in an inviscid incompressible flow.
Bernoullis equation can be used to approximate these parameters in water air or any fluid that has very low viscosity. In Bernoullis equation the total pressure of an ideal fluid is derived from the Conservation of Energy. Question 2 0 out of 5 points The.
If work is done internally Im not sure no energy is lost ie it is reversible. If a nuclide is known to decay then its decay equation is where Y is the nuclide having one more proton than X see Figure 4. Bernoullis equation is derived from the law of conservation of energy and work-energy theorem means work done between any two points or sections is equal to the change in energy of the system between those two points or sections.
The law of conservation of energy says that energy is neither created nor destroyed. First however I must be sure you have in mind the correct Bernoullis Principle. From what law do we derive Qin Qout from.
As the body is at height X from the ground PE mgX 5 Using 4 and 5 we get H2 is referred to the new height You may want to watch the following video on potential energy and kinetic energy to better understand the principle of conservation of energy 992187. Bernoullis equation considers only pressure and gravitational forces acting on the fluid particles. Learn vocabulary terms and more with flashcards games and other study tools.
The mass times the velocity of the center of mass is constant. 3 Energy cannot be created or destroyed. This demo works best if your mouth is very close to the top of the paper and the leading edge of the paper is held steady so as to prevent.
Therefore any increase in one form results in a decrease in the other. Gay Lussac s Law d. We derive this e.
1 The total amount of energy in the universe remains constant. Answer 1 of 5. Advertisement Expert-verified answer 45 5 108 flightbath Answer.
The Bernoullis equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids. Where p is the pressure exerted by the fluid v is the velocity of the fluid ρ is the density of the fluid and h is the height of the container. E2 is the new energy Where E mgH2 H2 is the new height.
2 Energy can be created or destroyed. In fact each term in the equation has units of energy per unit volume. Students use the associated activity to learn about the relationships between the components of the Bernoulli equation through.
Boyle s law B. The simplest form of Bernoullis equation steady and incompressible flow states that the sum of mechanical energy potential energy and kinetic energy along a streamline is constant. 5 In a closed isolated system energy is conserved.
No net force can be generated within the system since all internal forces occur in opposing pairs. It is quite simple but does take some explanation. Explain the restrictions of Bernoullis equation.
Conservation of energy is not saving energy. The law of conservation of energy can also be used in the analysis of flowing fluids. We change it from one form of energy into another.
What assumptions is Bernoullis Equation based on. We can prove this for the second term by substituting ρ m V into it and gathering terms. Question 1 5 out of 5 points Bernoullis equation can be derived from the conservation of.
Bernoullis equation can be considered a statement of the conservation of energy principle appropriate for flowing fluids. This lesson describes Bernoullis principle from several different perspectives appropriate for a range of age groups and lists a number of activities and demonstrations that use Bernoullis principle. Is motion of waves electrons atoms molecules substances and objects.
Bernoullis equation is a form of the conservation of energy principle. It is one of the most importantuseful equations in fluid mechanics. Bernoullis principle relates the pressure of a fluid to its elevation and its speed.
Start studying Balancing Equations and the Law of Conservation of Matter. Question 1 5 out of 5 points Bernoullis equation can be derived from the conservation of. Note that the second and third terms are the kinetic and potential energy with m replaced by ρ.
We saw that Bernoullis equation was the result of using the fact that any extra kinetic or potential energy gained by a system of fluid is caused by external work done on. The total angular momentum of the system is constant. The simplified form of Bernoullis equation can be summarized in the following memorable word equation.
Bernoullis equation can be viewed as a conservation of energy law for a flowing fluid. When we use energy it doesnt disappear. P 1 2 ρ v 2 ρ g h c o n s t a n t.
I find the explanations that start with conservation of energy to be unnecessarily complicated and confusing to the beginner. According to Bernoullis equation for steady ideal fluid flow principle of conservation of mass holds velocity and pressure are inversely proportional total energy is constant throughout the energy is constant along a stream-line but may vary across streamlines 4. No work is done by an external agent.
Conservation of Angular Momentum.

What Is Bernoulli S Equation Article Khan Academy

Pin By Ingeniero Garcia On Water Rockets Engineering Science Learn Physics Physics Experiments
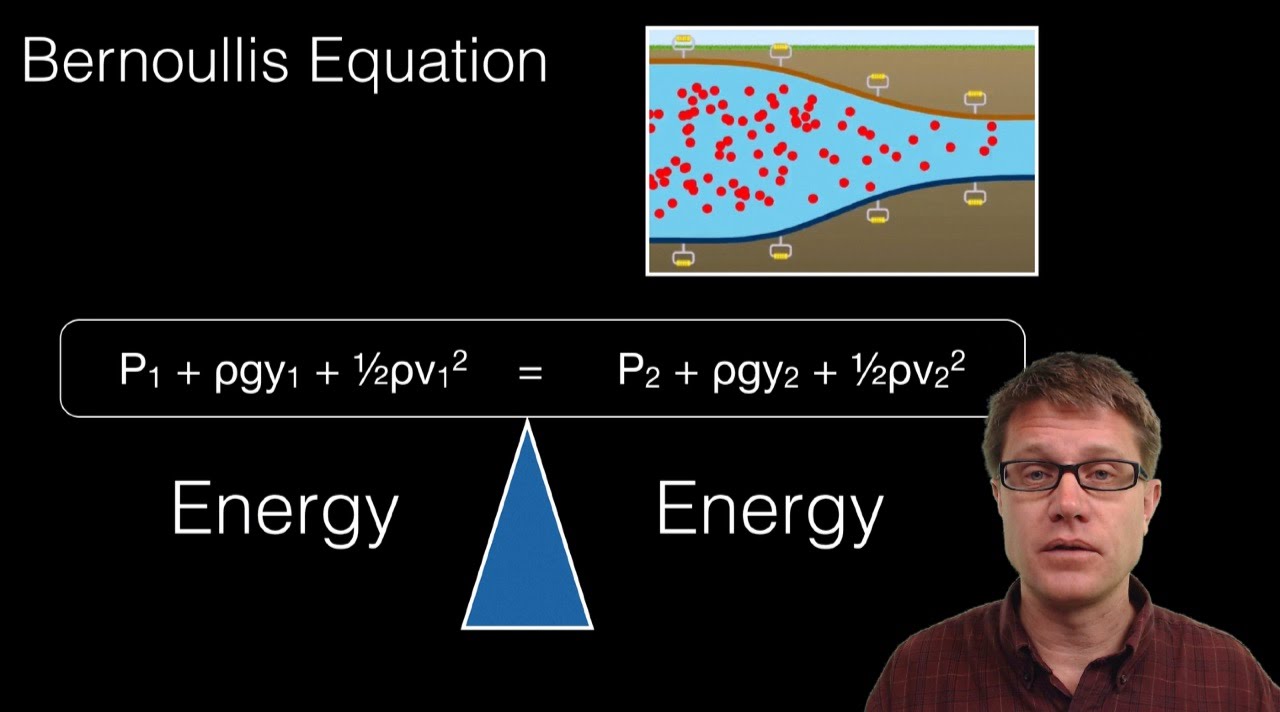

No comments for "What Best Describes the Conservation Law Associated With Bornoullis Equation"
Post a Comment